Nobody likes to be under pressure. And it doesn’t matter which one. Queen also sang about this together with David Bowie in their famous single “Under pressure.” What is pressure? How to understand pressure? How is it measured, by what instruments and methods, where is it directed and what does it press on? The answers to these and other questions are in our article about pressure in physics and not only.
Definition and formula of pressure
Definition
Pressure
is a physical quantity characterizing the state of a continuous medium.
It is equal to the limit of the ratio of the normal component of the force that acts on a section of the surface of a body with area $\Delta S$ to the size of a given area at $\Delta S \rightarrow 0$ . Pressure is indicated by the letter p. Then the mathematical notation for determining pressure will be the formula: $$p=\lim _{\Delta S \rightarrow 0} \frac{\Delta F_{n}}{\Delta S}=\frac{d F_{n}}{d S}$$
Expression (1) determines the pressure at a point.
How to reduce or increase blood pressure
A heavy crawler tractor produces a soil pressure of 40–50 kPa. A boy weighing 45 kg produces pressure only 3 times less than such a tractor. This is due to the large area of the tractor tracks.
Depending on the pressure they want to achieve, the area of the supports is reduced or increased. For example, in order to reduce the pressure of a building on the ground, during the construction process the area of the lower part of the foundation is increased.
Truck tires are much wider than passenger car tires. To verify this, pay attention to the wheels of some large truck. The widest tires can be seen on cars designed for driving in the desert. The same life hack is used in aircraft landing gear.
The inverse relationship is also used, for example, when creating blades for piercing and cutting tools. The sharp blade has a small area, so even a small pressure creates a lot of pressure.
Problem once
The book is on the table. The mass of the book is 0.6 kg. The area of its contact with the table is 0.08 m2. Determine the pressure of the book on the table.
Solution
A force equal to the weight of the book will press on the table. Since it is at rest, its weight will be equal to the force of gravity. Hence:
p = mg/S = 0.6 × 10 / 0.08 = 75 Pa
Answer: the pressure of the book on the table will be 75 Pa.
Problem two
The DT-75M tracked tractor weighing 6,610 kg has a supporting area of both tracks of 1.4 m2. Determine the pressure of this tractor on the soil.
Solution:
p = mg/S = 6,610 × 10 / 1.4 = 47,214 Pa = 47.2 kPa
Answer: the tractor pressure on the soil is 47.2 kPa.
Problem three
A man weighing 80 kg with a bag weighing 100 N stands motionless on the floor. The force of pressure of the soles of his shoes on the floor is uniformly distributed over an area of 600 cm2. How much pressure does the person exert on the floor?
Solution
Human mass: m = 80 kg.
Weight of the bag held by a person: Pc = 100 N.
Contact area of the sole of the boots with the floor: S = 600 cm2.
600 cm2 = 600 / 10,000 m2 = 0.06 m2
Pressure is the ratio of force to the area over which it acts. In this case, the force acting on the area is equal to the sum of the person’s gravity and the weight of the bag:
F = mg + Pс
Therefore, the pressure exerted by a person with a bag on the floor is equal to:
p = (mg + Pc) / S = (80 × 10 + 100) / 0.06 = 15,000 Pa = 15 kPa
Answer: the pressure of a person with a bag on the floor is 15 kPa.
Hydrostatic pressure
Hydrostatic pressure is the pressure inside a column of liquid or gas, found by the formula:
$$p=p_{0}+\rho gh(4)$$
where $\rho$ is the density of the substance, g=9.8 m/s2 is the acceleration of free fall, h is the height of the column of the substance. p0 – external pressure on gas or liquid.
The curvature of the surface layer of the liquid leads to the appearance of additional pressure on the liquid, then the pressure under the curved liquid is defined as:
$$p=p_{0}^{*}+2 \sigma H(5)$$
where $\mathrm{P}_{0}^{*}$ is the surface tension of the liquid, p0* is the pressure under the uncurved layer of liquid, H is the average curvature of the liquid surface, calculated according to Laplace’s law:
$$H=\frac{1}{2}\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)$$
R1, R2 – main radii of curvature.
10.1. Pressure calculation
Home / Publications / Literature / Bookshelf / Diver's HandbookIn diving practice, one often encounters the calculation of mechanical, hydrostatic and gas pressure over a wide range of values. Depending on the value of the measured pressure, different units are used.
In the SI and ISS systems, the unit of pressure is the pascal (Pa)
, in the MKGSS system - kgf/cm2 (technical atmosphere - at). Torus (mm Hg), atm (physical atmosphere), m water are used as off-system units of pressure. Art., and in English measures - pound/in2. The relationships between the various pressure units are given in Table 10.1.
Mechanical pressure is measured by the force acting perpendicularly per unit surface area of the body:
where p is pressure, kgf/cm2; F—force, kgf; S—area, cm2.
Example 10.1.
Determine the pressure that a diver exerts on the deck of the ship and on the ground underwater when he takes a step (i.e., stands on one leg).
The weight of a diver in equipment in air is 180 kgf, and under water 9 kgf. The area of the sole of the diving overshoe is 360 cm2. Solution. 1) Pressure transmitted by diving boots to the deck of the ship, according to (10.1): р = 180/360 = 0.5 kgf/cm
or in SI units
p = 0.5 * 0.98.105 = 49000 Pa = 49 kPa.
Table 10.1. Relationships between different units of pressure
2) Pressure transmitted by diving boots to the ground under water: or in SI units p = 0.025 * 0.98 * 105 = 2460 Pa = 2.46 kPa.
Hydrostatic pressure
liquid is everywhere perpendicular to the surface on which it acts, and increases with depth, but remains constant in any horizontal plane.
If the surface of the liquid does not experience external pressure (for example, air pressure) or is not taken into account, then the pressure inside the liquid is called excess pressure
where p is the fluid pressure, kgf/cm2; p—liquid density, gs” s4/cm2; g—gravitational acceleration, cm/s2; Y—specific gravity of liquid, kg/cm3, kgf/l; H - depth, m.
If the surface of the liquid experiences external pressure pp. then the pressure inside the liquid
If atmospheric air pressure acts on the surface of a liquid, then the pressure inside the liquid is called
absolute pressure
(i.e., pressure measured from zero - complete vacuum): where B is atmospheric (barometric) pressure, mm Hg.
Art. In practical calculations for fresh water, take Y = l kgf/l and atmospheric pressure p0 = 1 kgf/cm2 = 10 m of water. Art., then the excess water pressure in kgf/cm2 and the absolute water pressure Example 10.2.
Find the absolute pressure of sea water acting on a diver at a depth of 150 m if the barometric pressure is 765 mm Hg. Art., and the specific gravity of sea water is 1.024 kgf/l.
Solution.
Absolute pressure according to (10/4)
approximate value of absolute pressure according to (10.6) In this example, using the approximate formula (10.6) for calculation is quite justified, since the calculation error does not exceed 3%.
Example 10.3.
In a hollow structure containing air under atmospheric pressure pa = 1 kgf/cm2, located under water, a hole formed through which water began to flow (Fig. 10.1). How much pressure will the diver experience if he tries to close this hole with his hand? The cross-sectional area of the hole is 10X10 cm2, the height of the water column H above the hole is 50 m.
Rice.
9.20. Observation camera "Galeazzi": 1 - eye; 2 — cable release and cable cutting device; 3 — connection for telephone input; 4 — hatch cover; 5 — upper porthole; 6 — rubber seal ring; 7 — lower porthole; 8 — camera body; 9 — oxygen cylinder with pressure gauge; 10 — emergency ballast release device; 11 — emergency ballast; 12 — lamp cable; 13 - lamp; 14 — electric fan; 15—telephone-microphone; 16 — battery; 17 — regenerative working box; 18 — hatch cover porthole Solution.
Excess water pressure at the hole according to (10.5) P = 0.1-50 = 5 kgf/cm2.
Pressure force on the diver's hand from (10.1)
F = Sp = 10*10*5 = 500 kgf = 0.5 tf.
The pressure of the gas enclosed in a vessel is distributed evenly, if you do not take into account its weight, which, given the size of the vessels used in diving practice, has an insignificant effect. The pressure of a constant mass of gas depends on the volume it occupies and the temperature.
The relationship between gas pressure and its volume at a constant temperature is established by the expression
P1 V1 = p2V2 (10.7)
where р1 and р2 are the initial and final absolute pressure, kgf/cm2;
V1 and V2 - initial and final volume of gas, l. The relationship between gas pressure and its temperature at a constant volume is established by the expression
where t1 and t2 are the initial and final gas temperatures, °C.
At constant pressure, a similar relationship exists between the volume and temperature of the gas
The relationship between pressure, volume and temperature of a gas is established by the combined law of the gas state
. Example 10.4.
The capacity of the cylinder is 40 l, the air pressure in it according to the manometer is 150 kgf/cm2. Determine the volume of free air in the cylinder, i.e. the volume reduced to 1 kgf/cm2.
Solution.
Initial absolute pressure p = 150+1 = 151 kgf/cm2, final p2 = 1 kgf/cm2, initial volume V1 = 40 l.
Volume of free air from (10.7) Example 10.5.
The pressure gauge on the oxygen cylinder in a room with a temperature of 17°C showed a pressure of 200 kgf/cm2. This cylinder was transferred to the deck, where the next day at a temperature of -11 ° C its readings dropped to 180 kgf/cm2. There was a suspicion of an oxygen leak. Check whether the suspicion is correct.
Solution.
Initial absolute pressure p2 =200 + 1 = =201 kgf/cm2, final p2 = 180 + 1 = 181 kgf/cm2, initial temperature t1 = 17°C, final temperature t2 =—11°C. Calculated final pressure from (10.8)
Suspicions are unfounded, since the actual and calculated pressures are equal.
Example 10.6.
A diver underwater consumes 100 l/min of air compressed to a pressure of a diving depth of 40 m. Determine the free air consumption (i.e. at a pressure of 1 kgf/cm2).
Solution.
The initial absolute pressure at the immersion depth according to (10.6)
P1 = 0.1*40 =5 kgf/cm2.
Final absolute pressure P2 = 1 kgf/cm2
Initial air flow Vi = l00 l/min.
Free air flow according to (10.7)
The partial pressure of the gas
included in the air (artificial breathing mixture) is determined according to the nomogram in Fig. 10.2 or from the expression where pcm is the partial pressure of gas in the mixture, kgf/cm2; Pcm—absolute pressure of the gas mixture, kgf/cm2; C is the volumetric gas content in the mixture, %.
Example 10.7.
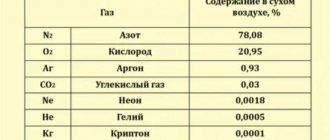
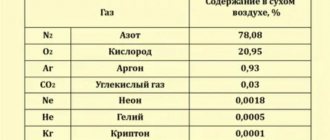
Determine the partial pressure of the gases included in the air supplied to the diver’s suit on the surface and at a depth of 40 m, if the analysis showed a nitrogen content of 79%, oxygen 20% and carbon dioxide 1%.
Solution.
The absolute air pressure on the surface is Рcm -1 kgf/cm2.
Rice. 10.2. Nomogram for determining the partial pressure of gas pg depending on the percentage of gas C and the absolute pressure of the gas mixture PCM
Partial pressure of gases on the surface according to (10.11): Approximately the same results can be obtained using the nomogram in Fig. 10.2.
Residual gas pressure in cylinders.
To obtain gas mixtures using the bypass method (see diagram a, Fig. 8.15), it is often necessary to know the residual pressure of the gas (oxygen) in the gas supply cylinder (cylinder K), which is equal to
where por is the residual absolute pressure of the gas (oxygen) in the supply cylinder, kgf /cm2;
Pcm is the absolute pressure of the gas mixture in the mixing cylinder, kgf/cm2; C is the gas (oxygen) content in the gas mixture by volume, %. Forward Contents Back
Barometric
This term refers to the pressure of the atmosphere (gravity) on all objects and objects found in it, including the surface of the Earth itself. Most people also know it as atmospheric.
It is considered a thermodynamic parameter, and its value varies depending on the place and time of measurement, as well as weather conditions and location above/below sea level.
The magnitude of barometric pressure is equal to the modulus of the atmospheric force over an area of one unit normal to it.
In a stable atmosphere, the magnitude of this physical phenomenon is equal to the weight of a column of air on a base with an area equal to one.
The normal barometric pressure is 101,325 Pa (760 mm Hg at 0 degrees Celsius). Moreover, the higher the object is from the surface of the Earth, the lower the air pressure on it becomes. Every 8 km it decreases by 100 Pa.
Thanks to this property, water in kettles boils much faster in the mountains than on the stove at home. The fact is that pressure affects the boiling point: as it decreases, the latter decreases. And vice versa. The operation of such kitchen appliances as a pressure cooker and autoclave is based on this property. The increase in pressure inside them contributes to the formation of higher temperatures in the vessels than in ordinary pans on the stove.
The barometric altitude formula is used to calculate atmospheric pressure. It looks like in the photo below.
P is the desired value at altitude, P0 is the air density near the surface, g is the free fall acceleration, h is the height above the Earth, m is the molar mass of the gas, t is the temperature of the system, r is the universal gas constant 8.3144598 J⁄(mol x K), and e is the Eichler number equal to 2.71828.
Often in the above formula for atmospheric pressure, K is used instead of R - Boltzmann’s constant. The universal gas constant is often expressed through its product by Avogadro's number. It is more convenient for calculations when the number of particles is given in moles.
When making calculations, you should always take into account the possibility of changes in air temperature due to a change in meteorological situation or when gaining altitude above sea level, as well as geographic latitude.
Measuring instruments
You can save time on calculations by using special devices that operate by determining the pressure in the corresponding environment, which is similar to a pressure gauge. Their differences lie in the operating instructions, scope of use, accuracy, and scope.
To determine blood pressure, you will need a barometer-type pressure gauge. To determine the vacuum (Pa less than atmospheric) you will need a different type of apparatus - a vacuum gauge. In humans, the indicator is determined using a sphygmomanometer. Most patients call this equipment a non-invasive blood pressure monitor.
Such devices are classified into the following subtypes:
- mercury mechanical;
- semi-automatic;
- automatic digital.
Their accuracy depends on the materials used in the manufacturing process and the measurement area. Some devices measure blood pressure and pulse simultaneously. They operate automatically from batteries. Due to the presence of a digital display, it is easy to find out the result. Mechanical ones are considered more accurate.
To determine P, you will need to put a cuff on the patient’s right arm. By holding the mechanism, the bulb is pumped. The maximum and minimum limits begin with the appearance and then the disappearance of a characteristic knocking sound. Gradually the mechanism weakens. To obtain accurate data, experience with a mechanical tonometer and attentiveness will be required. If pressure fluctuations in the air are observed, you will need a differential pressure gauge or pressure gauge.
Exact sciences
The unit of measurement of pressure in physics and chemistry is the letter “P” (translated into Latin as “pressūra”). If there is equilibrium inside and outside the cylinder walls, the indicator is designated “P”. The international system uses Pascals. Using the formula for fluid pressure and force, we can come to the conclusion that 1 Pa = 1 N/ 1 sq. m. Since the unit is small, it is difficult to use in calculations.
From the table of standard converters in physics, the following notations are more often used:
- Bars. 1 Bar=105 Pa.
- Torrs or mmHg (1 torr equals 133 Pa).
- mm water pillar
To determine pressure, force and area are used: P = mg / S. There is a dependence of the value on volume and mass. The indicator is characterized by the following property: the smaller the area, the greater the force exerted on the body. If the pressure does not change, but S increases, then the desired indicator decreases.
Absolute
This is the name of the total pressure under which a substance or object is located, without taking into account the influence of other gaseous components of the atmosphere.
It is measured in pascals and is the sum of excess and atmospheric pressure. It is also the difference between barometric and vacuum types.
It is calculated using the formula P = P2 + P3 or P = P2 - P4.
The starting point for absolute pressure under the conditions of planet Earth is the pressure inside the container from which air has been removed (that is, a classic vacuum).
Only this type of pressure is used in most thermodynamic formulas.
Hydraulic Press
A hydraulic press consists of two communicating cylindrical vessels. Pistons with areas S1 and S2 move in the vessels. The cylinders are filled with technical oil.
The volume of liquid displaced by the small piston enters the large cylinder.
A hydraulic press gives a gain in force as many times as the area of the larger piston is greater than the area of the smaller one. A hydraulic press does not provide any benefit in work.
In practice, due to the presence of friction: