Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
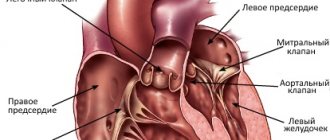
Работа и мощность сердца. Аппарат искусственного кровообращения
Работа, совершаемая сердцем, затрачивается на преодоление сил давления и сообщение крови кинетической энергии.
Рассчитаем работу, совершаемую при однократном сокращении левого желудочка. Изобразим
Vу
— ударный объем крови — в виде цилиндра (рис. 9.9). Можно считать, что сердце продавливает этот объем по аорте сечением
S
на расстояние
l
при среднем давлении
р.
Совершаемая при этом работа
На сообщение кинетической энергии этому объему крови затрачена работа
где r — плотность крови,u
— скорость крови в аорте. Таким образом, работа левого желудочка сердца при сокращении равна
Так как работа правого желудочка принимается равной 0,2 от работы левого, то работа всего сердца при однократном сокращении
Формула (9.17) справедлива как для покоя, так и для активного состояния организма. Эти состояния отличаются разной скоростью кровотока.
Подставив в формулу (9.17) значения
р
= 13 кПа,
Vy =
60 мл = 6 • 10 -5 м 3 , r = 1,05 • 10 3 кг/м 3 ,
u =
0,5 м/с, получим работу разового сокращения сердца в состоянии покоя:
Al »
1 Дж. Считая, что в среднем сердце совершает одно сокращение в секунду, найдем работу сердца за сутки:
Ас
= 86 400 Дж. При активной мышечной деятельности работа сердца может возрасти в несколько раз.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
|
График квадратичной функции — парабола, которая имеет следующий вид для y = x2:
Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов.
График функции y = –x2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -4 | -1 | 0 | -1 | -4 |
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.
Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.
Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.
Для наглядности возьмем функцию y = ax2 + bx + c, для построения которой нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Правила визуализации данных
Чтобы графики и диаграммы были понятны читателям, при их построении нужно соблюдать следующие рекомендации:
- Выбирайте правильный тип и формат визуализации информации. Используйте график, подходящий для ваших данных и соответствующий вашей цели. Например, если вам нужно отобразить динамику показателей, создайте обычный линейный график. В случае, когда предполагается сравнение нескольких категорий между собой, правильным выбором станет столбиковая (линейчатая) или секторная (круговая) диаграмма. Ориентируйтесь на количество категорий, если их у вас больше 5, лучше подойдет столбиковая, так как в круговой диаграмме с большим числом долей информацию считывать неудобно.
- Не нарушайте общепринятые стандарты, например, временные оси (года, месяцы, кварталы) всегда располагайте горизонтально слева направо, так как это интуитивно понятно для читателей и облегчит восприятие информации.
- Старайтесь делать дизайн диаграммы максимально простым и ясным. Не используйте элементы, которые могу отвлечь читателя от сути: градиентную заливку, тени, трехмерные эффекты и пр.
- Удаляйте с ваших диаграмм все неинформативные элементы, оставляйте только те, что действительно необходимы, так как загромождение графиков ненужной информацией значительно затрудняет их восприятие. К примеру, если у вас есть подписи значений, то линии сетки и ось уже не нужны, поскольку это дублирование информации. Если вы все же используете основные, а также вспомогательные линии сетки, делайте их как можно более простыми и не бросающимися в глаза. На первом плане должна быть важная информация, а не вспомогательные элементы.
- Визуализировать данные следует так, чтобы с первого взгляда были видны самые высокие и самые низкие значения, тенденции и корреляции. В противном случае нужно менять тип графика. Старайтесь сделать так, что было легко сравнить разные показатели и выявить соотношение, поэтому разбивать однотипную информацию на несколько отдельных графиков не стоит.
- Однако если необходимо визуализировать много различных типов данных и категорий, напротив, нужно разделить диаграмму на несколько частей. Например, на линейном графике нежелательно показывать больше четырех-пяти линий. Перегруженная информацией диаграмма только запутает читателя.
- Если на диаграмме отображаются категории, которые обычно ассоциируются с определенным цветом, к примеру, положительные значения – зеленый, отрицательные показатели – красный, а мужчины и женщины – голубой и розовый цвета, не стоит нарушать общепринятый порядок. Пользователю проще воспринимать эти категории в ожидаемой цветовой гамме.
- Если вы сравниваете показатели текущего и прошедшего года, можно сделать прошедший год более бледным, а текущий обозначить более ярко. Однако использовать следует оттенки одного цвета, чтобы было понятно, что речь идет об одном и том же показателе.
- Позаботьтесь о правильном форматировании чисел на диаграмме: в больших числах используйте разделители разрядов (то есть указывайте 1 000 000, а не 1000000) и убирайте лишние знаки после запятой. Это сделает числа легко читабельными.
- Учтите, что у диаграммы должно быть понятное, отражающее суть название и полная легенда, то есть все необходимые поясняющие подписи. Период времени и единицы измерения должны быть четко обозначены и трактоваться абсолютно однозначно, чтобы у читателей не возникало никаких вопросов, что изображено на диаграмме.
И еще пара советов: не используйте разные виды графиков и диаграмм для однотипных данных. Читателю требуется время, чтобы привыкнуть к каждому новому виду диаграммы и понять, что обозначает определенная линия или столбик, поэтому всегда выбирайте одинаковые диаграммы для данных одного типа. Кроме того, следует придерживаться одной цветовой гаммы в одном отчете или презентации. Хорошее решение – использование цветов вашего корпоративного стиля.
Уравнение квадратичной функции имеет вид y = ax2 + bx + c.
Разберем общий алгоритм на примере y = 2×2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2×2 + 3x — 5.
D = b2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
√D = 7
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2×2 + 3x — 5 = 0
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
- Нанести эти точки на координатную плоскость и построить график параболы:
Построение графиков в Excel по данным таблицы
В MS Excel есть возможность не только проводить вычисления, используя разные формулы, но и также строить на их основе различные диаграммы: гистограммы, круговые диаграммы, точечные и т.д. В этом уроке мы разберем, для чего применяют графики. И так, графики – это разновидность диаграммы, схожая с гистограммой. Они бывают трех видов: простой, график с накоплением и нормированный график с накоплением. Каждый из этих графиков бывает двух видов: с маркером и без. Так эти два вида строятся одинаково, рассмотрим только маркированные графики. Коротко опишем применение каждого графика, и далее на примерах разберем более подробно, как их построить. a) Простой график нужен для того, чтобы изобразить, как изменяется некое значение во времени (прибыль по месяцам; рождаемость по годам и т.д.). b) График с накоплением показывает, как изменяется составляющая целого значения с течением времени. (Лучше использовать диаграмму с накоплением) c) Нормированный график с накоплением показывает изменение доли каждого значения с течением времени. Есть еще объемный график, который схож с простым графиком. Поэтому мы покажем только его конечный вид.
Уравнение квадратичной функции имеет вид y = a * (x — x₀)2 + y₀
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2×2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x — 1)2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить y = x2,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
- Построить график параболы для каждого случая.
Простая диаграмма
Рассмотрим простой график на примере таком примере прибыли некоторой фирмы по 3 товарам за определенный период. Для этого выделим нужные нам ячейки, как на рисунке ниже.
Теперь строим простой маркированный график. Для этого выделяем диапазон В1:D6, на главное ленте выбираем Вставка–Диаграммы (нажимаем на стрелочку справа сверху). В появившемся окне выберем нужную нам диаграмму. В первом случае – простой график. Нажимаем ОК.
Выбираем график слева, т.к. он показывает изменение прибыли во времени. Если вы все сделали правильно, то должно получиться так, как на рисунке ниже:
Итак, диаграмма построена, но на ней не отображаются года. Изменить название диаграммы очень просто. Нужно нажать на заголовок и ввести подходящее название. Например, Прибыль по товарам в 2010-214 гг. Для того, чтобы года отображались на оси Х, необходимо нажать на ось правой кнопкой мыши для вызова контекстного меню и нажать Выбрать данные.
После этого появится такое окошко:
Изменяем подписи горизонтальной оси. Должно открыться такое окошко:
Нажимаем туда, где выделено красным и выбираем диапазон. В нашем случае это А2:А6. И нажимаем клавишу Enter и ОК. В результате этого должно открыться предыдущее окно, но выглядеть будет следующим образом:
Нажимаем ОК, меняем название диаграммы. Теперь она должна выглядеть так:
Осталось добавить подписи данных. В версии Excel 2013–2016 это делается очень просто. Нажимаем на плюсик справа, который вызывает различные команды и ставим галочку Название осей. Должно получиться так:
Как и в случае с названием, ставим курсор в область каждой из осей и подписываем их согласно условию. Например, ось Х – Год, ось Y – Прибыль. Должно получиться так, как на рисунке ниже:
В MS Excel версиях 2007-2010 форматировать оси, область диаграммы и т.д. с помощью дополнительной вкладки на ленте Работа с диаграммами.
Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)
Рассмотрим следующий пример: y = (x — 2) * (x + 1).
Как строим:
- Данный вид уравнения позволяет быстро найти нули функции:
(x — 2) * (x + 1) = 0, отсюда х₁ = 2, х₂ = -1.
- Определим координаты вершины параболы:
- Найти точку пересечения с осью OY:
с = ab =(-2) * (1)= -2 и ей симметричная.
- Отметим эти точки на координатной плоскости и соединим плавной прямой.
Формула любви
Женщины всегда привлекали мужчин. Одаренная мужская половина посвящала им стихи, музыку, песни, картины, дарила звезды, украшения, квартиры, машины, дачи, ноутбуки. Не оставались в стороне и математики. Но что мог математик приподнести возлюбленной самое-самое свое дорогое? Ну, конечно же, — новую Формулу Любви! Первые такие формулы были, естественно, графические. Ведь тысячелетия назад математические записи отсутствовали и наиболее распространенными были геометрические изображения. Вот один математик-астроном подарил невесте траектрию движения планеты Венеры, которую можно наблюдать в течение 8 лет только с Земли:
В центре этого красивого узора можно заметить стилизованные контуры пяти мелких сердец. Далее сердца укрупняются Еще дальше пошел неизвестный любитель геометрии с еще более впечатляющим орнаментом:
Сердец тут уже намного больше и контуры их ясней. Первые алгебраические формулы любви были, конечно же, примитивными:
https://lovestih.ru/wp-content/uploads/2011/07/formula-lubvi.jpg
Как говорится, любовь на уровне первоклассника. Но совсем уж опустились двоечники или недоучки, пошедшие прямой дорожкой не в науку, а в бизнес. Вот полюбуйтесь хотя бы на это:
Ну, куда годится такая формула? Даже гиганты символьной математики Maple или Mathcad, такое безобразие не берут!
ФОРМУЛА ЛЮБВИ 1
Лишь в 18 веке пришло понимание того, что пора уже дарить женщинам более сложные формулы — с элементарными функциями и другими прибамбасами. Такими, например, как полярные координаты. Первой кривой, отдаленно напоминающей сердце, была кардиоида.
В системе Maple любой желающий может проверить верность уравнения, скопировав следующие команды:
plot(1-cos(t-(1/2)*Pi), t = 0 .. 2*Pi, color = red, coords = polar, thickness = 5);
Кардиоида впервые встречается в трудах французского учёного Луи Карре в далеком 1705 году. Название кривой дал Джованнии Сальвемини ди Кастиллоне в 1741 году. Вычисление длины кривой выполнил Де Ла Ир, который независимо открыл кардиоиду в 1708 году (он еще известен своими удивительными исследованиями магических квадратов). Также независимо описал кардиоиду голландский математик Й. Коерсма ( 1741 г.). В дальнейшем к кривой проявляли интерес многие видные математики XVIII-XIX веков. Конечно, эта кривая описывает контур довольно несуразного сердца. Какого-то явно больного или жирного.
ФОРМУЛА ЛЮБВИ 2
Чтобы поправить положение, некий ловкий математик чуточку усложнил формулу кардиоиды и получил нечто более человеческое:
В системе Maple:
plot((1-sin(t))*(1/2+(1/7)*tanh(50*sin(t))*abs(sin(2*t)))/(1+(.5*sin(t)-1)^2), t = -Pi .. Pi, color = red, coords = polar, thickness = 5);
И вот тут началась гонка! Математики словно с цепи сорвались и стали соревноваться друг с другом: кто же найдет формулу, описывающую самое красивое сердце! Эту захватывающую гонку можно понаблюдать, если в Яндексе набрать ключевые слова “Формула любви” и просмотреть 22 тысячи рисунка. Для верности можно и погуглить. Итак, я буду излагать упомянутую гонку по возрастающей качества графиков.
ФОРМУЛА ЛЮБВИ 3
Внутри сердечка записано уравнение в декартовых координатах. Однако, когда я стал строить график, то появилось ужасно много лишних линий. Поэтому пришлось переводить в полярные координаты (два уравнения даны сверху). Не верите – проверьте:
with(plots): F := plot(sqrt((sin(t)^4+cos(t)^2)*(1+sqrt(1-sin(t)^4-cos(t)^2)))/(sin(t)^4+cos(t)^2), t = 0 .. Pi, color = red, coords = polar, thickness = 5): G := plot(sqrt(-(sin(t)^4+cos(t)^2)*(-1+sqrt(1-sin(t)^4-cos(t)^2)))/(sin(t)^4+cos(t)^2), t = Pi .. 2*Pi, color = red, coords = polar, thickness = 5): display();
Увидев это один супер-мупер математик под ником doctor по аналогии построил объемный вариант токого же сердца. У меня прога не получилась, поэтому верю ему на слово и привожу картинку из инета: https://math-4-fun.blogspot.com/2010/11/heart-curve.html
Ну не чудеса? Наверное, любимая девушка doctor’а долго прыгала от счастья и больше не ходила к нему на прием в связи с выздоровлением.
ФОРМУЛА ЛЮБВИ 4