Basic Concepts
A function is a dependency of "y" on "x", where "x" is the variable or argument of the function and "y" is the dependent variable or value of the function.
Defining a function means defining a rule according to which, based on the values of the independent variable, its corresponding values can be found. Here are the ways you can set it:
- Tabular method. Helps you quickly determine specific values without additional measurements or calculations.
- Graphic method: visually.
- Analytical method, through formulas. It is compact and possible to calculate the function for an arbitrary value of the argument from the domain of definition.
- Verbal method.
The graph of a function is the union of all points, when instead of “x” you can substitute arbitrary values and find the coordinates of these points.
Work and power of the heart. Heart-lung machine
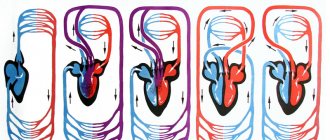
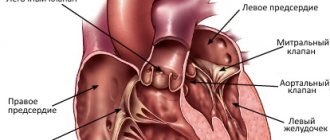
The work done by the heart is spent on overcoming pressure forces and communicating kinetic energy to the blood.
Let's calculate the work done during a single contraction of the left ventricle.
Let's depict Vу
- stroke volume of blood - in the form of a cylinder (Fig. 9.9).
We can assume that the heart pushes this volume along the aorta with a cross-section S
to a distance
l
at an average pressure
p.
The work done
Work is required to impart kinetic energy to this volume of blood
where r is blood density, u
- blood speed in the aorta. Thus, the work of the left ventricle of the heart during contraction is equal to
Since the work of the right ventricle is taken to be equal to 0.2 of the work of the left, then the work of the entire heart during a single contraction
Formula (9.17) is valid for both rest and the active state of the body. These conditions are distinguished by different blood flow rates.
Substituting into formula (9.17) the values
p
= 13 kPa,
Vy =
60 ml = 6 • 10 -5 m 3, r = 1.05 • 10 3 kg/m 3,
u =
0.5 m/s, we obtain the work of one-time contractions of the heart at rest:
Al »
1 J. Assuming that on average the heart makes one contraction per second, we find the work of the heart per day:
Ac
= 86,400 J. With active muscular activity, the work of the heart can increase several times.
Construction of a quadratic function
The quadratic function is given by the formula y = ax2 + bx + c , where x and y are variables, a, b, c are given numbers, the mandatory condition is a ≠ 0. The equation has the following distribution:
|
The graph of a quadratic function is a parabola, which looks like this for y = x2:
Points marked with green circles are called base points . To find their coordinates for the function y = x2, you need to make a table:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
If in the equation of a quadratic function the leading coefficient is equal to one, then the graph has the same shape as y = x2 for any values of the remaining coefficients.
The graph of the function y = –x2 looks like an inverted parabola:
Let's fix the coordinates of the base points in the table:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -4 | -1 | 0 | -1 | -4 |
Looking at both graphs, you can notice their symmetry with respect to the OX axis. Let us note the important conclusions:
- If the leading coefficient is greater than zero a > 0, then the branches of the parabola are directed upward.
- If the leading coefficient is less than zero a < 0, then the branches of the parabola are directed downward.
How to graph a quadratic function - consider the values of x where the function is zero. Otherwise, these can be called function zeros. On the graph, the zeros of the function f(x) are the points of intersection of y = f(x) with the OX axis.
Since the ordinate (y) of any point on the OX axis is zero, therefore, to find the coordinates of the points of intersection of the graph of the function y = f(x) with the OX axis, you need to solve the equation f(x) = 0.
For clarity, let’s take the function y = ax2 + bx + c, to construct which we need to solve the quadratic equation ax2 + bx + c = 0. In the process, we will find the discriminant D = b2 - 4ac, which will give us information about the number of roots of the quadratic equation.
Let's consider three cases:
- If D < 0, then the equation has no solutions and the parabola has no points of intersection with the OX axis. If a > 0, then the graph looks like this:
- If D = 0, then the equation has one solution, and the parabola intersects the OX axis at one point. If a > 0, then the graph looks like this:
- If D > 0, then the equation has two solutions, and the parabola intersects the OX axis at two points, which can be found as follows:
If a > 0, then the graph looks something like this:
Based on the above, it is clear that knowing the direction of the branches of the parabola and the sign of the discriminant, we have an understanding of what the graph of a particular function will look like.
The coordinates of the vertex of the parabola are also an important parameter of the graph of a quadratic function and are found in the following way:
The axis of symmetry of a parabola is a straight line that passes through the vertex of the parabola parallel to the OY axis.
To build a graph, we need the point of intersection of the parabola with the OY axis. Since the abscissa of each point of the OY axis is equal to zero, in order to find the point of intersection of the parabola y = ax2 + bx + c with the OY axis, you need to substitute zero in the equation instead of x: y(0) = c. That is, the coordinates of this point will correspond to: (0; c).
The image shows the main parameters of the graph of a quadratic function:
Data Visualization Rules
To ensure that graphs and diagrams are understandable to readers, the following recommendations must be followed when constructing them:
- Choose the right type and format for information visualization. Use a graph that is appropriate for your data and fits your purpose. For example, if you need to display the dynamics of indicators, create a regular line graph. In cases where several categories are expected to be compared with each other, the correct choice would be a bar (bar) or pie (pie) chart. Focus on the number of categories; if you have more than 5, a bar chart is better, since it is inconvenient to read information in a pie chart with a large number of shares.
- Do not violate generally accepted standards, for example, always place time axes (years, months, quarters) horizontally from left to right, as this is intuitive for readers and will facilitate the perception of information.
- Try to keep your diagram design as simple and clear as possible. Do not use elements that can distract the reader from the essence: gradient fills, shadows, 3D effects, etc.
- Remove all uninformative elements from your diagrams, leaving only those that are really necessary, since cluttering graphs with unnecessary information greatly complicates their perception. For example, if you have value labels, then the gridlines and axis are no longer needed, since this is duplication of information. If you do use major and minor grid lines, keep them as simple and unobtrusive as possible. Important information should be in the foreground, not auxiliary elements.
- Data should be visualized so that the highest and lowest values, trends, and correlations are visible at a glance. Otherwise, you need to change the graph type. Try to make it easy to compare different indicators and identify the relationship, so you should not split the same type of information into several separate graphs.
- However, if you need to visualize many different types of data and categories, in contrast, you need to divide the chart into several parts. For example, on a line chart it is not advisable to show more than four or five lines. A chart that is overloaded with information will only confuse the reader.
- If the chart displays categories that are typically associated with a particular color, such as positive values being green, negative values being red, and men and women being blue and pink, don't break the rules. It is easier for the user to perceive these categories in the expected color scheme.
- If you compare the indicators of the current and last year, you can make the past year paler and the current one more vivid. However, shades of the same color should be used so that it is clear that we are talking about the same indicator.
- Take care to format the numbers in the chart correctly: for large numbers, use place separators (that is, enter 1,000,000 rather than 1,000,000) and remove extra decimal places. This will make the numbers easy to read.
- Please note that the diagram must have a clear title that reflects the essence and a full legend, that is, all the necessary explanatory captions. The time period and units of measurement should be clearly indicated and interpreted in an absolutely unambiguous manner so that readers do not have any questions about what is depicted in the diagram.
And a couple more tips: do not use different types of graphs and charts for the same type of data. It takes time for the reader to get used to each new type of chart and understand what a particular line or bar means, so always choose the same charts for the same type of data. In addition, you should stick to one color scheme per report or presentation. A good solution is to use the colors of your corporate style.
The equation for a quadratic function is y = ax2 + bx + c.
Let's look at the general algorithm using the example y = 2×2 + 3x - 5.
How we build:
- Let us determine the direction of the branches of the parabola. Since a = 2 > 0, the branches of the parabola are directed upward.
- Let's find the discriminant of the quadratic trinomial 2×2 + 3x - 5.
D = b2 - 4ac = 9 - 4 * 2 * (-5) = 49 > 0
√D = 7
In this case, the discriminant is greater than zero, so the parabola has two points of intersection with the OX axis. To find their coordinates, we solve the equation:
2x2 + 3x – 5 = 0
- Parabola vertex coordinates:
- The point of intersection with the OY axis is: (0; -5) and is symmetrical to it.
- Plot these points on the coordinate plane and plot the parabola:
Building graphs in Excel using table data
In MS Excel, it is possible not only to carry out calculations using different formulas, but also to build various charts based on them: histograms, pie charts, scatter charts, etc. In this lesson we will look at what graphs are used for. And so, graphs are a type of chart, similar to a histogram. They come in three types: simple, stacked and normalized stacked. Each of these graphs comes in two types: with and without a marker. So these two types are constructed in the same way, let’s consider only the labeled graphs. We will briefly describe the use of each graph, and then, using examples, we will look in more detail at how to construct them. a) A simple graph is needed to depict how a certain value changes over time (profit by month; birth rate by year, etc.). b) A stacked graph shows how the component of an integer value changes over time. (It is better to use a stacked chart) c) A normalized stacked chart shows the change in the proportion of each value over time. There is also a volumetric chart, which is similar to a simple chart. Therefore, we will only show its final form.
The equation of a quadratic function is y = a * (x - x₀)2 + y₀
Coordinates of its vertex: (x₀; y₀). In the equation of a quadratic function y = 2×2 + 3x - 5 with a = 1, then the second coefficient is an even number.
Let's look at an example: y = 2 * (x - 1)2 + 4.
How we build:
- Let's use linear transformation of function graphs. For this you will need:
- construct y = x2,
- multiply the ordinates of all points on the graph by 2,
- move it along the OX axis 1 unit to the right,
- move it along the OY axis 4 units up.
- Draw a graph of the parabola for each case.
Simple diagram
Let's look at a simple graph using this example of the profit of a certain company for 3 products for a certain period. To do this, select the cells we need, as in the figure below.
Now let's build a simple labeled graph. To do this, select the range B1:D6, on the main ribbon select Insert–Charts (click on the arrow at the top right). In the window that appears, select the diagram we need. In the first case, a simple graph. Click OK.
We select the graph on the left, because it shows the change in profit over time. If you did everything correctly, it should look like the picture below:
So, the chart is built, but the years are not displayed on it. Changing the title of a chart is very easy. You need to click on the title and enter a suitable name. For example, Profit by goods in 2010-214. In order for the years to be displayed on the X-axis, you need to right-click on the axis to open the context menu and click Select data.
After this, the following window will appear:
Change the labels of the horizontal axis. The following window should open:
Click where it is highlighted in red and select the range. In our case, this is A2:A6. And press the Enter key and OK. As a result, the previous window should open, but it will look like this:
Click OK and change the name of the diagram. It should now look like this:
All that remains is to add data signatures. In Excel 2013–2016, this is done very simply. Click on the plus sign on the right, which calls up various commands and check the Axes name box. It should look like this:
As in the case of the name, we place the cursor in the area of each of the axes and label them according to the condition. For example, the X axis is Year, the Y axis is Profit. It should look like the picture below:
In MS Excel versions 2007-2010, format axes, chart area, etc. using an additional tab on the Work with Charts ribbon.
The equation of a quadratic function is y = (x + a) * (x + b)
Consider the following example: y = (x - 2) * (x + 1).
How we build:
- This type of equation allows you to quickly find the zeros of a function:
(x - 2) * (x + 1) = 0, hence x₁ = 2, x₂ = -1.
- Let's determine the coordinates of the vertex of the parabola:
- Find the point of intersection with the OY axis:
c = ab =(-2) * (1)= -2 and it is symmetrical.
- Let's mark these points on the coordinate plane and connect them with a smooth straight line.
Love Formula
Women have always attracted men. The gifted male half dedicated poems, music, songs, paintings to them, gave them stars, jewelry, apartments, cars, dachas, laptops. Mathematicians did not stand aside either. But what could a mathematician give his most precious gift to his beloved? Well, of course, a new Formula of Love! The first such formulas were, naturally, graphic. After all, thousands of years ago there were no mathematical records and the most common were geometric images. Here is one mathematician-astronomer who gave the bride the trajectory of the planet Venus, which can be observed for 8 years only from Earth:
In the center of this beautiful pattern you can see the stylized outlines of five small hearts. Further, the hearts are enlarged. An unknown lover of geometry went even further with an even more impressive ornament:
There are much more hearts here and their outlines are clearer. The first algebraic formulas for love were, of course, primitive:
https://lovestih.ru/wp-content/uploads/2011/07/formula-lubvi.jpg
As they say, love is at the level of a first grader. But the poor students or half-educated students have completely sunk, taking the direct path not to science, but to business. Just take a look at this:
Well, where does this formula fit? Even the giants of symbolic mathematics Maple or Mathcad do not accept such disgrace!
FORMULA OF LOVE 1
Only in the 18th century did it become understood that it was time to give women more complex formulas - with elementary functions and other bells and whistles. Such, for example, as polar coordinates. The first curve that vaguely resembled a heart was a cardioid.
In the Maple system, anyone can check the accuracy of the equation by copying the following commands:
plot(1-cos(t-(1/2)*Pi), t = 0 .. 2*Pi, color = red, coords = polar, thickness = 5);
Cardioid was first encountered in the works of the French scientist Louis Carré back in 1705. The name of the curve was given by Giovanni Salvemini di Castillone in 1741. The calculation of the curve length was carried out by De La Hire, who independently discovered the cardioid in 1708 (he is also known for his amazing studies of magic squares). The Dutch mathematician J. Koersma (1741) also independently described the cardioid. Subsequently, many prominent mathematicians of the 18th-19th centuries showed interest in the curve. Of course, this curve describes the outline of a rather awkward heart. Someone obviously sick or fat.
FORMULA OF LOVE 2
To improve the situation, some clever mathematician complicated the cardioid formula a little and got something more human:
In the Maple system:
plot((1-sin(t))*(1/2+(1/7)*tanh(50*sin(t))*abs(sin(2*t)))/(1+(.5* sin(t)-1)^2), t = -Pi .. Pi, color = red, coords = polar, thickness = 5);
And then the race began! Mathematicians seemed to have broken free and began to compete with each other: who will find the formula that describes the most beautiful heart! You can watch this exciting race if you type the keywords “Formula of Love” in Yandex and view 22 thousand pictures. To be sure, you can google it. So, I will outline the mentioned race in increasing quality of graphs.
FORMULA OF LOVE 3
Inside the heart is an equation written in Cartesian coordinates. However, when I started building a graph, an awful lot of extra lines appeared. Therefore, we had to convert it to polar coordinates (two equations are given above). If you don't believe me, check it out:
with(plots): F := plot(sqrt((sin(t)^4+cos(t)^2)*(1+sqrt(1-sin(t)^4-cos(t)^2)) )/(sin(t)^4+cos(t)^2), t = 0 .. Pi, color = red, coords = polar, thickness = 5): G := plot(sqrt(-(sin(t )^4+cos(t)^2)*(-1+sqrt(1-sin(t)^4-cos(t)^2)))/(sin(t)^4+cos(t)^ 2), t = Pi .. 2*Pi, color = red, coords = polar, thickness = 5): display();
Having seen this, one super-mathematician under the nickname doctor, by analogy, built a three-dimensional version of the same heart. The program didn’t work out for me, so I take his word for it and here’s a picture from the internet: https://math-4-fun.blogspot.com/2010/11/heart-curve.html
Well, not miracles? Probably, the doctor’s beloved girlfriend jumped for a long time with happiness and no longer went to see him due to her recovery.
FORMULA OF LOVE 4